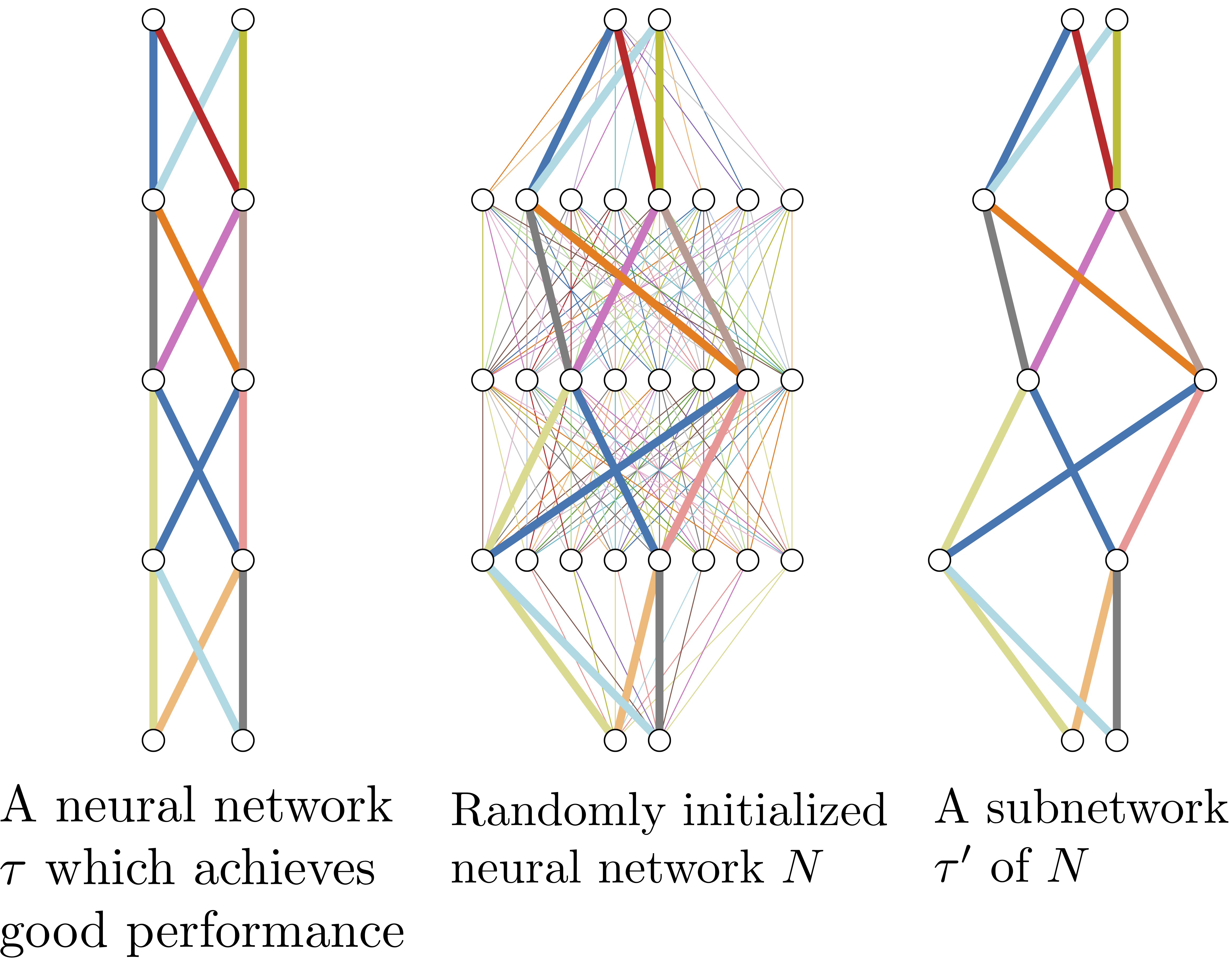
Figure 1. If a neural network with random weights (center) is sufficiently overparameterized, it will contain a subnetwork (right) that perform as well as a trained neural network (left) with the same number of parameters.
In recent years, there's been a bizarre line of work in deep learning that shows you can get remarkable results by just using the random features in a neural network—as in, you don't need to train the network; you can just use the network at initialization! However, you do need to do something on top of the network to get something interesting out of it.
Here's a brief summary and the thoughts it has inspired as I've been reading along. These are mostly notes to my future self but might be of interest to others interested in how deep neural networks work.
- This work grew out of the subfield of pruning/sparsity in neural networks.
- Someone noticed that so-called lottery tickets would do better than random chance before even being trained.
- This paper was probably the first to make the bold claim/observation that "masking is training". They called these Supermasks.
- Someone else worked on a surprisingly simple algorithm to simultaneously train and prune.
- Usually this doesn't work, but it seems like the key for them was probably that they were greatly constraining the set of weights that could be pruned; they were only pruning in the "pointwise convolution" layer of a MobileNetV1.
- The paper has a lot of extraneous stuff it doesn't need, but it is kind of interesting that they try to draw an equivalency between pruning and NAS. But I would say it's a small subset of NAS, in fact.
- The above two ideas can be combined to train not the network itself, but only a mask on top of the network!
- They were able to achieve quite good performance this way (never as good as training the dense network itself, but often as good as training a network with equivalent size/sparsity).
- There's also someone who proved this is possible, in principle (and that's the unfortunate namesake of this post).
- This is also obviously very related to reservoir computing, which I've been learning about lately (if you're familiar with that concept).
- A kinda funny follow-on paper, Supermasks in Superposition, used this concept to avoid catastrophic forgetting by training a different mask for each task.
- In this case they just used a randomly initialized network, but others have done this on top of pretrained networks and shown them to be competitive with fine-tuning, for the purposes of transfer learning.
- They also claim that "the entire, growing set of supermasks can be stored in a constant-sized reservoir by implicitly storing them as attractors in a fixed-sized Hopfield network." At that point, this starts to sound like a hypernetwork!
- All this learning of masks also seems related to a paper from my own lab, Learning to Continually Learn, which employs an architecture where one network learns to apply a mask to another network (referred to as neuromodulation). The way this is different, however, is that the mask is not static, but rather conditioned on each input.
- I'm also seeing this as intimately related to the intriguing paper, Training BatchNorm and Only BatchNorm. Similar to the mask-learning idea, we can also keep all parameters of the network fixed except for the scale+shift parameters in each BatchNorm layer of a typical convnet.
- This works surprisingly well, similar to the masks. Another interesting thing they notice when you do this is that you get a lot of the scale parameters going to zero—in other words, this is also learning to prune!
- Combining the two ideas above, there are also works which use affine transforms as neuromodulators, rather than a simple binary mask (called FiLM layers). These are used for transfer/multi-task learning (similar to the SupSup paper above), and for conditional ("style") GANs, among other things.
- In some very modern cases, the modulations are even produced by a separate network, bringing us back around to the connection to hypernetworks!
It's been very interesting to read about all the surprising things you can do with random recombinations of existing features. It colors my perspective on pre-trained models a bit differently, and the training procedure itself. Is SGD really taking the network weights very far away from their initialization? Is it even doing much more than pruning?
But going further, I'm not just interested in sparse networks, but how existing neurons or layers could learn to connect to each other, in a self-organized growing/shaping process more similar to what happens in the development of a real brain. So I'm looking for ways to establish new connections, not just remove pre-existing ones. But that could be its own separate post, so I'll just close with one last reference that forms somewhat of a bridge from here to there:
- A more modern option for simultaneous training and pruning is RigL.
- I really like this algorithm because it incorporates aspects of "growing" new connections, not just pruning existing ones. (Although the other algorithms also allow connections to come and go, but this one seems to have a more explicit difference between pruning and growing.)
